Welcome to a new series of basic training articles written by Bob Johnson. These brief pieces seek to provide practical down-to-earth guidance on a range of engineering topics. The subject matter will vary from basic engineering principles all the way through to the Finite Element Analysis (FEA) of assemblies.
Why is Bob presenting this material? Briefly, he is one half of the consultancy and training company, DAMT, and specialises in the reliable analysis of complex assemblies such as offshore connectors.
Bob provides the NAFEMS training course on basic FEA and considers that well-thought-out FEA can accurately mimic the real world and add tangible value to the design process.
Outside of engineering he has completed the last nine London marathons (four of which in under three hours) and this year was third Vet50 in the Ben Nevis fell race (2hrs 2mins) and third Vet50 in the 3-Peaks Cyclo-Cross (3hrs 51mins). To top all this, in 2006 he completed the London Marathon whilst dressed as a 6ft (32lb) Dalek!
Down to business
All engineering calculations need to be carried out in a sensible and consistent set of units. Don’t think that errors with units are a thing of the past: the $125 million Mars Climate Orbiter (launched 1998) was sent 60 miles closer to the Martian surface because thruster data was supplied in pounds-force instead of Newtons! This article seeks to show the advantage of the metric system of units (as used by NASA and not its supplier in this case!) and provides examples of how one set of units can be converted to any other consistent set without the need for a crib sheet.
Any calculation that we care to undertake will need to respect a consistent system of units. Any answer we quote must contain (a) the numerical calculation and (b) the outcome of a study of the units involved. Mistakes in either part will invalidate the overall result but that said mistakes in the units are more embarrassing!
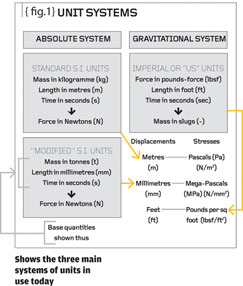
Fig #1: Shows the three main systems of units in use today
{Fig #1} shows the three main systems of units in use today. On the left, two “absolute” systems and on the right one “gravitational” system of units.
Most engineers agree that an “absolute” system of units is best because the base quantities (in the S.I. system: mass, length and time) are always the same wherever you are. (Note that the base quantities in the Imperial (US) system are length, time and force – the force varies depending on the local gravitational field so would not be applicable on the moon). Even US text books consider that we will all use an absolute system such as S.I. one day!
Concentrating on absolute systems, then Figure #1 shows the standard S.I. system (kg, m, s, N) and the so-called “modified” S.I. system (tonnes, mm, s, N). The “modified” system is in common use today because calculations will render displacements in millimetres and stresses in Newtons-per-square millimetre (easily stated as Mega-Pascals or MPa). The stresses have a sensible magnitude in that, for instance, the yield stress of a piece of steel might be 400MPa in the modified S.I. system (as opposed to 400 million Newtons per square metre in the standard S.I. system).

Fig #2: Unity brackets are simply equations expressed in a quotient format
{Fig. #2} introduces the concept of “Unity Brackets” and these allow us to convert one unit for (say) distance into any other unit for distance.
For example, we can easily make a unity bracket from the relationship that 25.400mm is exactly equal to one inch. We can convert the above “equation” into the quotient form of [25.4mm / 1 inch] or [1 inch / 25.4mm]. In Figure 2 (and here in the text) the quotient is shown within square brackets to remind us that the value is one – thus the name “unity bracket”.
Figure #2 illustrates how unity brackets can be formed from a number of simple expressions. All we are doing is making a quotient such that the top equals the bottom!

{Fig #3:} Demonstrates how unity brackets can be used to convert one system of units to any other
{fig.3} demonstrates how these unity brackets can be used to convert one system of units to any other. The first example shows how the 3.528 litre capacity of a Rover V8 engine can be converted to cubic-inches (say for consumption of an interested party in the ‘States!).
In this example three unity brackets are used – note that two of which are cubed. Remember that one to any power is still one so all we’re doing here is multiplying the capacity in litres by one, three times. If we arrange our string of unity brackets such that cancelling can occur then we’re left with the capacity in cubic inches.
Figure #3 shows a further example which uses five unity brackets to convert from a motor torque of 140Nm to the Imperial equivalent of 103 lbsf-ft. Please study the examples – it really is an excellent system and endorsed by the Institute of Mechanical Engineers so it must be good! More next time – don’t have nightmares!
Coming up in Bob’s Engineering Workshop next month: forces, reactions and free-body diagrams.
Bob can be contacted at {encode=”bj@damt.co.uk” title=”bj@damt.co.uk”}
Bob Johnson shows the benefits of metric






